트리(Tree)
0. 요약
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
class Tree {
constructor() {
this.root = null;
this.size = 0;
}
// 노드 추가하기
add(data) {
const root = this.root;
const node = new Node(data);
if (!root) {
this.size++;
this.root = node;
return;
}
const searchTree = (parents) => {
if (data < parents.data) {
if (parents.left) return searchTree(parents.left);
else return (parents.left = node);
} else if (data > parents.data) {
if (parents.right) return searchTree(parents.right);
else return (parents.right = node);
} else return null;
};
this.size++;
searchTree(root);
}
// 노드 탐색하기
search(data) {
const root = this.root;
if (!root) return null;
let depth = 0;
const searchNode = (node, parents) => {
if (data < node.data) {
if (!node.left) return null;
depth++;
return searchNode(node.left, node);
} else if (data > node.data) {
if (!node.right) return null;
depth++;
return searchNode(node.right, node);
} else return { node, depth, parents };
};
return searchNode(root, null);
}
// 같은 레벨의 노드 구하기
getSameLevel(level) {
const arr = [];
const searchNode = (node, depth) => {
if (!node) return;
if (depth === level) return arr.push(node);
else {
searchNode(node.left, depth + 1);
searchNode(node.right, depth + 1);
}
};
searchNode(this.root, 0);
return arr;
}
// 특정 노드에서 다른 노드로 이동하는 경로 구하기
getPath(from, to) {
const from_node = this.search(from);
if (!from_node) {
return null;
}
let path = [];
let cur_node = from_node.node;
let edge = 0;
let loop = true;
while (loop) {
if (cur_node.data < to) cur_node = cur_node.right;
else cur_node = cur_node.left;
if (!cur_node) {
return null;
} else if (cur_node.data === to) {
loop = false;
} else {
path.push(cur_node);
}
edge++;
}
return {
from: from_node,
to: this.search(to),
edge,
path,
};
}
}1. 개요
2. 트리란?
2-1. 트리에서 사용되는 용어

2-2. 트리의 특징
3. 트리의 종류
3-1. 이진 트리(Binary Tree)

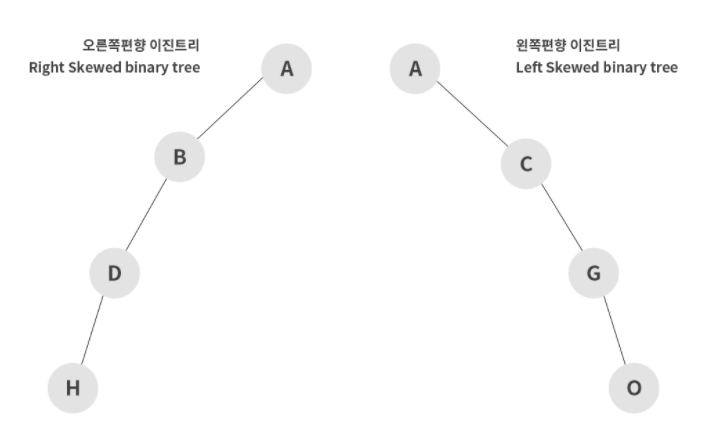
3-2. 편향 이진 트리(Skewed Binary Tree)
3-3. 포화 이진 트리(Perfect Binary Tree)

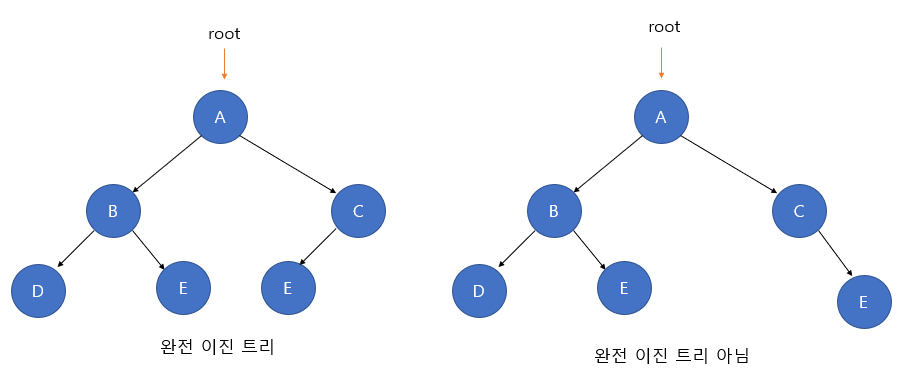
3-4. 완전 이진 트리(Complete Binary Tree)
3-5. 이진 탐색 트리(Binary Search Tree)


4. 트리의 순회
4-1. 전위 순회(Preorder)

4-2. 중위 순회(Inorder)

4-3. 후위 순회(Postorder)

5. 연결 리스트로 이진 탐색 트리 구현하기
5-1. 연결 리스트와 이진 탐색 트리의 기본 구조
5-2. 노드 추가하기
5-3. 노드 탐색하기
5-4. 같은 레벨의 노드 구하기
5-5. 특정 노드에서 다른 노드로 이동하는 경로 구하기
6. Conclusion
출처
Last updated