그래프(Graph)
0. 요약
0-1. 인접 리스트로 무방향 그래프 구현하기
class Graph {
constructor() {
this.vertices = new Map();
}
// 정점 추가하기
add(vertex) {
if (!this.vertices.get(vertex)) {
this.vertices.set(vertex, []);
}
}
// 정점 삭제하기
remove(vertex) {
if (this.vertices.get(vertex)) {
const v = this.vertices.get(vertex);
v.forEach((item) => {
this.vertices.set(
item,
this.vertices.get(item).filter((item) => item !== vertex)
);
});
this.vertices.delete(vertex);
return v;
}
}
// 정점의 존재여부 확인하기
contains(vertex) {
return this.vertices.has(vertex);
}
// 간선 연결하기
connect(from, to) {
if (this.contains(from) && this.contains(to)) {
if (this.vertices.get(from).includes(to)) return;
this.vertices.set(from, [...this.vertices.get(from), to]);
this.vertices.set(to, [...this.vertices.get(to), from]);
}
}
// 간선 삭제하기
disconnect(from, to) {
if (this.contains(from) && this.contains(to)) {
this.vertices.set(
from,
this.vertices.get(from).filter((item) => item !== to)
);
this.vertices.set(
to,
this.vertices.get(to).filter((item) => item !== from)
);
}
}
// 간선 존재여부 확인하기
hasEdge(from, to) {
if (this.contains(from) && this.contains(to)) {
const edges = this.vertices.get(from);
return edges.includes(to);
}
return false;
}
}0-2. 인접 행렬로 방향 그래프 구현하기
1. 개요
2. 그래프란?
2-1. 그래프에서 사용되는 용어
2-2. 그래프의 특징
3. 그래프의 종류
3-1. 무방향 그래프(Undirected Graph)

3-2. 방향 그래프(Directed Graph)

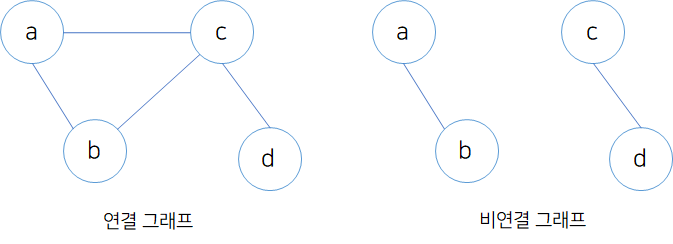
3-3. 연결 그래프(Connected Graph)
3-4. 비연결 그래프(Disconnected Graph)
3-5. 완전 그래프(Complete Graph)
3-6. 가중치 그래프(Weight Graph)
3-7. 사이클(Cycle)
3-8 비순환 그래프(Acyclic Graph)

4. 그래프의 구현방법
5. 인접 리스트로 무방향 그래프 구현하기
5-1. 그래프의 기본 구조
5-2. 정점 추가하기
5-3. 정점 삭제하기
5-4. 정점의 존재여부 확인하기
5-5. 간선 연결하기
5-6. 간선 삭제하기
5-7. 간선 존재여부 확인하기
6. 인접 행렬로 방향 그래프 구현하기
6-1. 그래프의 기본 구조
6-2. 정점의 존재여부 확인하기
6-3. 간선 연결하기
6-4. 간선 삭제하기
6-5. 간선 존재여부 확인하기
6-6. 차수 구하기
7. Conclusion
참고
Last updated